# Gráficos y Tablas
## Análisis exploratorio y corrección de errores detectados
No siempre vamos a poder realizar de forma tan sencilla la detección de errores, sobre todo cuando tenemos un gran volumen de datos, algo habitual en ciencia de datos. Por tanto, para poder detectar problemas presentes en los datos, es necesario llevar a cabo un análisis exploratorio de los mismos a través de gráficos y tablas.
Algunas de las funciones más útiles para este propósitos son:
**`summary(dataFrame)`**: Ofrece un resumen de todas las variables presentes en el conjunto de datos. Para las variables numéricas, muestra valor mínimo, máximo, media, mediana y primer y tercer cuartil; mientras que para las variables de tipo factor, muestra los 6 niveles mayoritarios, junto con sus frecuencias. En ambos casos se muestra además el número de casos perdidos.
**`pysch::describe(Filter(is.numeric,dataFrame))`**: Esta función ofrece más medidas de las variables numéricas como la desviación estándar y el índice de simetría
**`table(varCuali), prop.table()`**: Muestra la tabla de frecuencias de la variable cualitativa seleccionada.
**`hist(varCuant)`**: Muestra el histograma de la variable cuantitativa seleccionada.
**`barplot(table(varCuali))`**: Muestra el diagrama de barras de la variable cualitativa seleccionada.
A partir de estas funciones es posible hacerse una idea muy clara de cómo son las variables del conjunto de datos y de sus problemas. Para ello es importante fijarse en los siguientes aspectos:
1. **Límites de las variables cuantitativas:** Una forma rápida de verificar que las variables cuantitativas toman valores lógicos, es verificar que el máximo y el mínimo de las variables se encuentran dentro de los límites que marque la variable (por ejemplo, las variables que representan porcentajes deben situarse entre 0 y 100 o medidas como el peso, la altura, la edad, etc tomarán un número positivo).
2. **Niveles de las variables cualitativas**: En línea con el punto anterior, también debemos verificar que los niveles de las variables cualitativas tienen sentido, teniendo en cuenta el significado de las mismas.
3. **Número de datos perdidos**: Este tema lo veremos con mas detalle en el Tema 3, pero si en una variable observamos muchos datos faltantes (más de la mitad), es recomendable rechazarla al inicio del proceso, pues carece de suficiente información.
4. **Datos perdidos codificados**: En ocasiones, en lugar de deja "huecos" para representar los datos faltantes, se utiliza algún tipo de codificación que facilite el envío y la lectura de los conjuntos de datos. Ejemplo: En variables cualitativas el símbolo ? o el clásico NSNC (no sabe/no contesta) y en variables cuantitativas, el valor -1 (si la variable no puede tomar valores negativos) o 999. Es fundamental detectar este aspecto para poder analizar de manera correcta la presencia de ausentes.
5. **Frecuencia de las categorías de las variables cualitativas**: Dado que los modelos predictivos se basan en detectar patrones en las variables input que nos permitan aproximar el valor de la variable objetivo, es imprescindible que todos los niveles de las variables cualitativas estén bien representados pues, de los contrario, se podrían detectar patrones que no fueran extrapolbles al estar basados en muy pocas observaciones. Por ello, se debe verificar que la frecuencia de todas ellas sea superior al 2-5% (el porcentaje exacto depende del número de observaciones del conjunto de datos).
## Tablas
Vamos a construir una base de datos sencilla para ver este apartado
```r
#Definición de variables
edad=c(18,19,NA,18,24,17,22,15,22,25)
sexo=c(0,1,0,0,1,0,0,1,1,0)
estudios=c(1,2,0,1,3,2,3,1,2,3)
#Recodificamos como factores el sexo y el nivel de estudios asignando etiquetas:
sexo=factor(sexo, levels=c(0,1),
labels=c("Hombre","Mujer"))
estudios=factor(estudios, levels=c(0,1,2,3),
labels=c("Sin estudios","Estudios Primarios",
"Estudios Secundarios","Estudios Superiores"))
```
### Tablas de frecuencias unidemensionales
Construimos las tablas de frecuencias para la variable edad
**`table()`**: frecuencias absolutas
**`prop.table(table())`**: frecuencias relativas
```r
table(sexo)
# sexo
# Hombre Mujer
# 6 4
prop.table(table(sexo))
# sexo
# Hombre Mujer
# 0.6 0.4
```
### Tablas de frecuencias cruzadas
Las tablas cruzadas también se construyen usando **`table()`**y **`prop.table()`**especificando las dos variables a representar. En **`prop.table()`** incluimos un 1 si las queremos por filas, un 2 si por columnas, o nada si queremos las frecuencias relativas globales
```r
t=table(estudios,sexo)
## sexo
## estudios Hombre Mujer
## Sin estudios 1 0
## Estudios Primarios 2 1
## Estudios Secundarios 1 2
## Estudios Superiores 2 1
prop.table(t)
## sexo
## estudios Hombre Mujer
## Sin estudios 0.1 0.0
## Estudios Primarios 0.2 0.1
## Estudios Secundarios 0.1 0.2
## Estudios Superiores 0.2 0.1
prop.table(t,1)
## sexo
## estudios Hombre Mujer
## Sin estudios 1.000000 0.000000
## Estudios Primarios 0.666667 0.333333
## Estudios Secundarios 0.333333 0.666667
## Estudios Superiores 0.666667 0.333333
prop.table(t,2)
## sexo
## estudios Hombre Mujer
## Sin estudios 0.166667 0.000000
## Estudios Primarios 0.333333 0.250000
## Estudios Secundarios 0.166667 0.500000
## Estudios Superiores 0.333333 0.250000
```
¿Qué porcentaje de los hombres tiene estudios primarios? ¿Qué porcentaje de los que tienen estudios secundarios son mujeres?
### Tablas de frecuencias de una variable continua agrupada por intervalos
Una tabla de frecuencia para una variable continua no tiene sentido, veamos que pasa si representamos la edad (es discreta pero nos vale para este ejemplo) con una tabla de frecuencia:
```r
table(edad)
# 15 17 18 19 22 24 25
# 1 1 2 1 2 1 1
```
No nos está dando informacióm adicional ni resumiendo la variable. Para trabajar este tipo de variables, podemos construir intervalos. Primero vamos a ver los valores entre los que se sitúa la variable con la función **`range()`** y luego vamos a construir los intervalos de edad usando la **regla de Sturges**, que nos proporciona un número adecuado de intervalos en función del rango de los datos**`nclass.Sturges()`**y finalmente utilizando la función **`cut()`** para que nos construya una nueva variable que recodifica la edad en dichos intervalos.
```r
range(edad,na.rm=TRUE) # na.rm=TRUE para que ignore la presencia de valores perdidos
## [1] 15 25
nclass.Sturges(edad)
## [1] 5
seq(15,25,length=nclass.Sturges(edad))
## [1] 15.0 17.5 20.0 22.5 25.0
intervalosEdad=cut(edad,breaks=seq(15,25,length=nclass.Sturges(edad)),include.lowest=TRUE)
intervalosEdad
## [1] (17.5,20] (17.5,20] (17.5,20] (22.5,25] [15,17.5] (20,22.5]
## [8] [15,17.5] (20,22.5] (22.5,25]
## Levels: [15,17.5] (17.5,20] (20,22.5] (22.5,25]
```
Ahora ya podemos construir la tabla de frecuencias de esta variable:
```r
table(intervalosEdad)
## intervalosEdad
## [15,17.5] (17.5,20] (20,22.5] (22.5,25]
## 2 3 2 2
```
El paquete **`agricolae`** incluye la función **`table.freq()`** que construye la tabla de frecuencias para variables agrupadas en intervalos a partir de la información generada por la función **`hist()`** del paquete base de R.
```r
#install.packages("agricolae")
library(agricolae)
tbFreqEdad=table.freq(hist(edad,plot=FALSE))
tbFreqEdad
```
```
## Lower Upper Main Frequency Percentage CF CPF
## 1 14 16 15 1 11.1 1 11.1
## 2 16 18 17 3 33.3 4 44.4
## 3 18 20 19 1 11.1 5 55.6
## 4 20 22 21 2 22.2 7 77.8
## 5 22 24 23 1 11.1 8 88.9
## 6 24 26 25 1 11.1 9 100.0
```
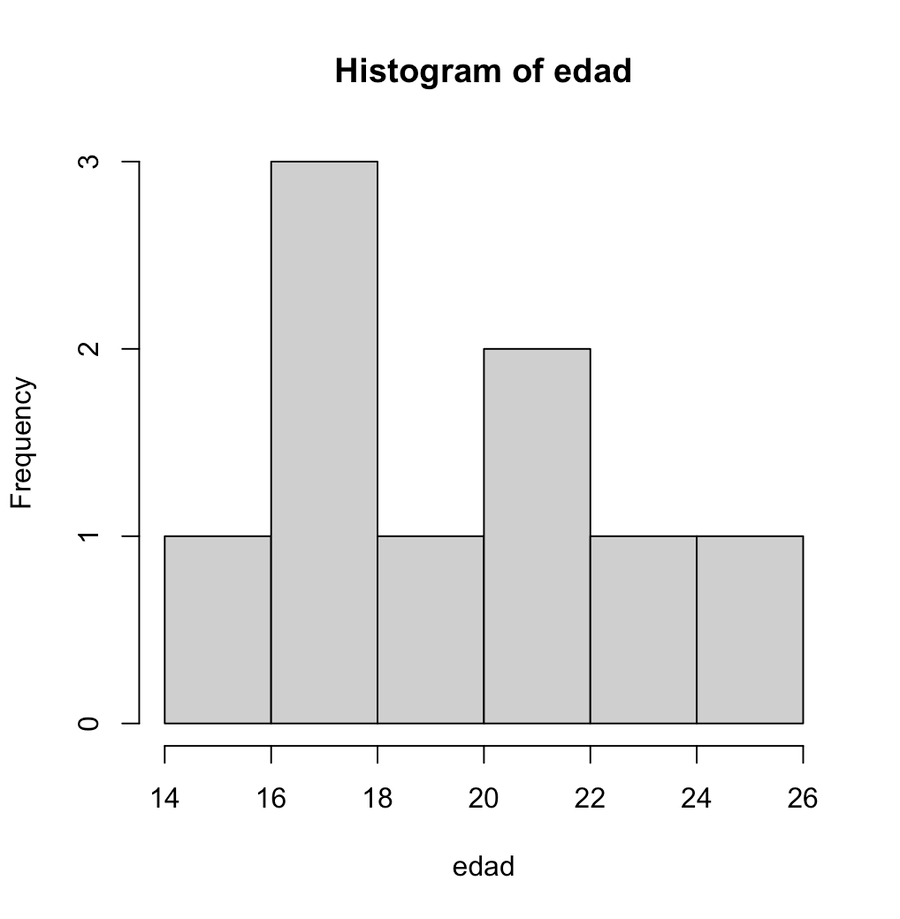
### Descriptivos
De la misma forma que podemos hacer tablas de frecuencias, podemos llevar a cabo una resumen descriptivo de las variables que contiene un **`data.frame`** con **`summary()`**
```r
misDatos=data.frame(edad,estudios,sexo)
summary(misDatos)
## edad estudios sexo
## Min. :15 Sin estudios :1 Hombre:6
## 1st Qu.:18 Estudios Primarios :3 Mujer :4
## Median :19 Estudios Secundarios:3
## Mean :20 Estudios Superiores :3
## 3rd Qu.:22
## Max. :25
## NA's :1
```
También podemos calcular media y desviación típica de la variable *edad* por *sexo* con la función **`aggregate()`**
```r
aggregate(edad,by=list(sexo),mean)
## Group.1 x
## 1 Hombre NA
## 2 Mujer 20
```
En el caso de los hombres nos encontramos con el problema de los valores perdidos. Para obtener el resultado prescindiendo de dichos valores, es preciso utilizar la opción **`na.rm=TRUE`**
```r
aggregate(edad,by=list(sexo),mean,na.rm=TRUE)
## Group.1 x
## 1 Hombre 20
## 2 Mujer 20
```
La librería **`psych`** contiene las funciones **`describe()`** y **`describeBy()`** que no sólo calculan la media sino que añaden otros estadísticos de interés
```r
#install.packages("psych")
library(psych)
describe(edad)
describeBy(edad,sexo,na.rm=TRUE)
```
## Gráficos
Estos serían las cuatro representaciones gráficos más sencillas para las variables que estamos viendo:
```
pie(table(estudios))
```
```
barplot(table(sexo))
```
```
hist(edad)
```
```
boxplot(edad~sexo)
```
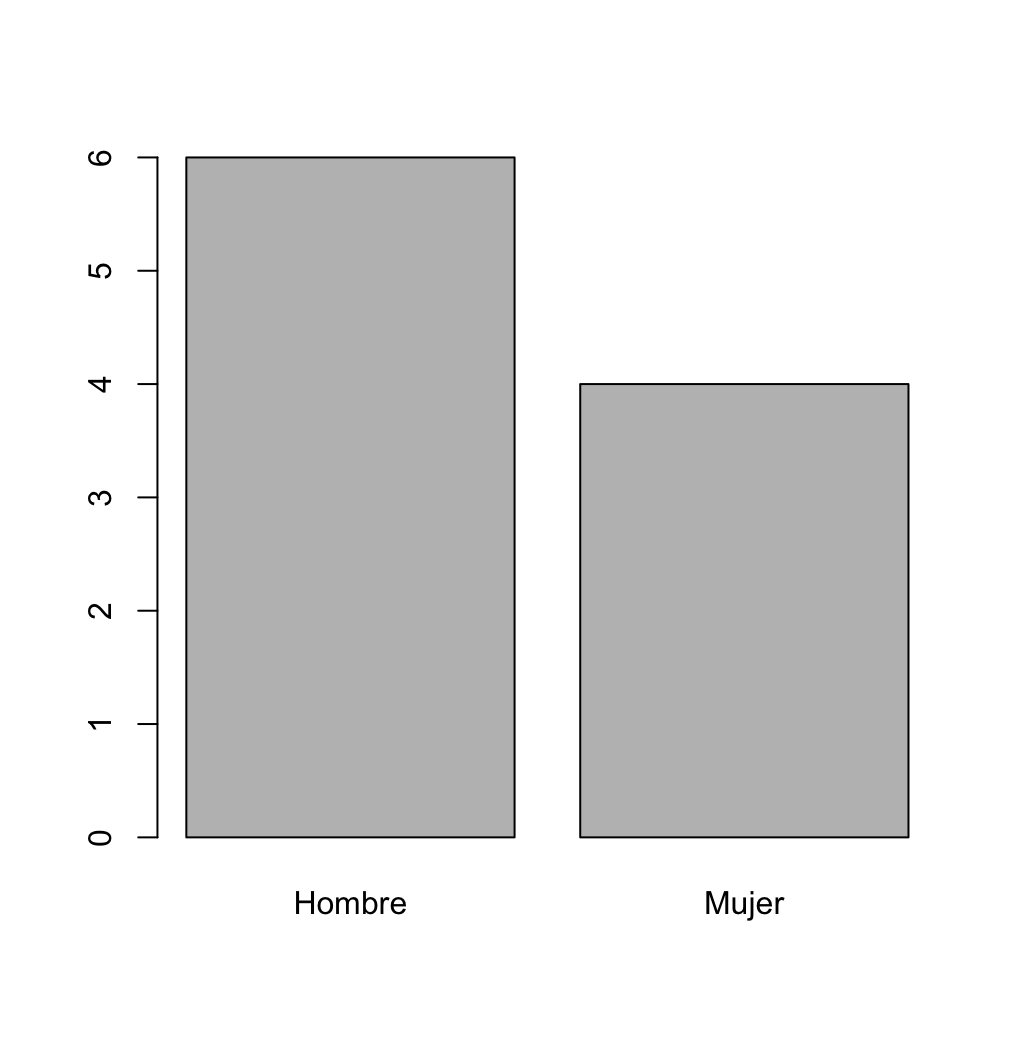
Ahora es tu turno: Realiza los siguientes ejercicios:
{% content-ref url="/pages/WmLzsgPz2I9hNlji864i" %}
[Ejercicios](/depuracion-de-datos-tfg3/tema-1-analisis-exploratorio-de-datos/graficos-y-tablas/ejercicios.md)
{% endcontent-ref %}
---
# Agent Instructions: Querying This Documentation
If you need additional information that is not directly available in this page, you can query the documentation dynamically by asking a question.
Perform an HTTP GET request on the current page URL with the `ask` query parameter:
```
GET https://silvia-pineda.gitbook.io/depuracion-de-datos-tfg3/tema-1-analisis-exploratorio-de-datos/graficos-y-tablas.md?ask=
```
The question should be specific, self-contained, and written in natural language.
The response will contain a direct answer to the question and relevant excerpts and sources from the documentation.
Use this mechanism when the answer is not explicitly present in the current page, you need clarification or additional context, or you want to retrieve related documentation sections.