Detección y tratamiento de datos atípicos

Un dato atípico, llamado outlier en inglés, es un valor de una de las variables que se observan en un conjunto de datos, que se diferencia de forma notable de los valores que toma dicha variable. También podemos considerar que los datos atípicos son observaciones cuyo comportamiento es distinto del comportamiento medio del resto de observaciones.

El problema de los datos atípicos es que distorsionan de forma importante los análisis en los que interviene la variable que contiene dichos datos.

Es muy importante no confundir un dato atípico con un dato erróneo. Por ejemplo una persona que mida 2.1 metros, aunque poco frecuente, no tiene porque tratarse de valor erróneo, pues se trata de un valor válido, y será un dato atípico si se compara con otros individuos de menor altura, pero no si forma parte de un conjunto de datos de jugadores de baloncesto. Es importante tratar primero los errores y luego los datos atípicos, como estamos viendo en esta asignatura.

Ejemplo

En un grupo de 10 personas, se observan para cada una de ellas las siguientes variables:

Tiempo: tiempo que tarda en recorrer 1.5 millas (en minutos)

Oxigeno: cantidad de oxígeno que absorve por minuto (en ml. por Kg de peso)

Tiempo=c(11.37,10.07,8.65,8.17,9.22,11.63,11.95,10.85,13.08,8.63)

Oxigeno=c(44.609,45.313,54.297,59.571,49.874,44.811,45.681,49.091,39.442,60.055)

data<-data.frame(Tiempo,Oxigeno)

Ajustamos una recta de regresión a estos datos

summary(glm(data$Tiempo~data$Oxigeno))

$$Tiempo = 21.32 - 0.2224*Oxigeno$$

Y lo representamos gráficamente

library(ggplot2)

ggp <- ggplot(data,aes(Tiempo, Oxigeno)) + geom_point()

ggp + stat_smooth(method = "lm",
formula = y ~ x,
 geom = "smooth")

Supongamos que en algún momento se ha producido un error y que en la observacion 10, el Tiempo = 18:

Tiempo=c(11.37,10.07,8.65,8.17,9.22,11.63,11.95,10.85,13.08,18)

Oxigeno=c(44.609,45.313,54.297,59.571,49.874,44.811,45.681,49.091,39.442,60.055)

data_outlier<-data.frame(Tiempo,Oxigeno)

Y volvemos a ajustar una recta de regresión y la volvemos a dibujar

$$Tiempo=10.26+0.02112*Oxigeno$$

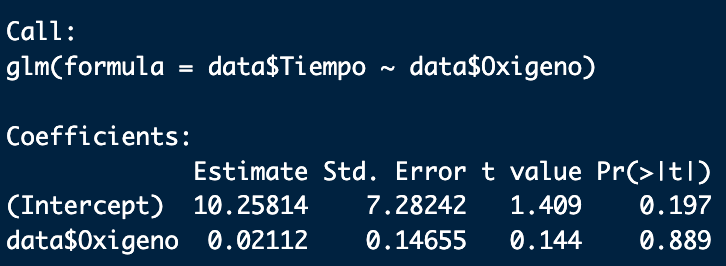
Los cambios producidos por una única observación son catastróficos. Para evitar estas situaciones, necesitamos estudiar la causa de estos valores y realizar un tratamiento de los mismos.

Vamos a realizar los siguientes ejercicios:

Ejercicios

Lo primero que nos preguntamos es ¿Qué clase de dato atípico tenemos?

Clases de datos atípicos

Tipos	Soluciones
Datos que son errores en la toma de datos o en la codificación de los mismos	Subsanar el error y si no es posible eliminar el dato y considerarlo “missing”
Datos causados por acontecimientos extraordinarios, pero su presencia está justificada	Mantenerlos salvo que su relevancia sea anecdótica
Observaciones extrañas para las que no nos sirve ningún tipo de justificación	Elimirlos cuando no es posible encontrar una explicación
Datos con valores extremos	El investigador decidirá si debe eliminarse o considerarlo representativo de una parte minoritaria. Si se elimina, debe quedar constancia y ser informada

Como criterio general, la decisión de los atípicos a eliminar, debe ser en función de sus características y de los objetivos del análisis a realizar.

A veces se analizan los datos con los atípicos y sin los atípicos para ver dicha influencia. Si los resultados son similares entonces se convierte en una decisión intranscendente lo que se haga con los atípicos. Pero si no los son, unos pocos valores atípicos no eliminados de un análisis pueden provocar que el resto de los datos resulten inútiles para llegar a conclusiones correctas.

Los datos atípicos los estudiaremos dentro del contexto de todas las variables. A veces, un valor extremo no es significativo dentro de un conjunto de variables. Por lo tanto, podemos abordar el problema desde el punto de vista univariante y multivariante.

Enfoque univariante

Para una variable continua, un dato atípico se determina por aquellas observaciones que caigan fuera de 1.5*IQR y un dato extremo para los que esta distancia sea superior a 3 veces el IQR, siendo IQR el Rango Intercuartílico que es la diferencia entre el cuartil tercero y el cuartil primero.

$$IQR=Q3-Q1$$

Es decir, aquellos puntos que están fuera de los bigotes de un diagrama de cajas

Vamos a utilizar la base de datos ozone de R para ilustrar el tema

10KB

ozone.csv

Lo primero sería ver el tipo de datos y que no haya errores e incongruencia como hemos visto en el Tema 1.

data <- read.csv("ozone.csv")  # import data

str(data)
summary(data)

Los meses y días de la semana podríamos pensar en convertirlos en variables categóricas, pero también las podemos dejar como numéricas. Siempre dependera de cómo queramos trabajar con ellas y sobre todo, representarlas.

Para el resto de variables, no tenemos NAs ni parece que haya errores.

Vamos a ver los outliers:

Vamos a estudiar la variable Pressure_height obteniendo los datos atípicos y extremos:

boxplot(data$Pressure_height)



###Los valores atípicos son:

outlier_values <- boxplot.stats(data$Pressure_height)$out  # outlier values.

out_ind <- which(data$Pressure_height %in% c(outlier_values))



###Los valores extremos son:

extreme_values <- boxplot.stats(data$Pressure_height,coef=3)$out  # extreme values.

ext_ind <- which(data$Pressure_height %in% c(extreme_values))



mtext(paste("Outliers: ", paste(outlier_values, collapse=", ")), cex=0.6)

La decisión de que hacer es más compleja, no siempre hay que borrar los datos atípicos o extremos, a veces basta con que seamos conscientes y en el posterior análisis tengamos en cuenta la influencia de los mismos. Otras veces dependerá del contexto del estudio y lo que queramos hacer después.

Además tenemos que tener en cuenta la proporción de datos atípicos o extremos en la muestra, es decir, si los datos representan menos de un 2-5% de la muestra, podríamos considerar borrarlos, si son más entonces los consideramos datos "típicos"

length(out_ind)/length(data$Pressure_height)*100
[1] 2.463054

En este ejemplo nos salen que los datos atípicos de la variable pressure height corresponden a un 2.5% de los datos, por tanto ya que son sólo atípicos y no extremos y están por encima del 2% vamos a dejarlos sin borrar pero siendo conscientes en futuros análisis de su existencia.

Enfoque bivariante

El caso bivariado, nos permite representar una variable en función de otra. Por ejemplo, en el caso de una variable continua en función de una variable categórica, volvemos a hacer uso del diagrama de cajas.

Variable continua con variable categórica

Ahora vamos a ver si la variable Pressure_height toma valores atípicos de la misma forma que antes al representarla por meses (Month) y días de la semana (Day_of_week):

par(mfrow=c(1, 2))

boxplot(data$Pressure_height ~ data$Month, main="Pressure Height across months") 

boxplot(data$Pressure_height ~ data$Day_of_week, main="Pressure Height for days of week")  

dev.off()

En el gráfico primero, donde se representa la variable Pressure_height por la variable Month, sólo 3 atípicos son detectados que no son los mismos que se detectaban en la variable en cuestión, y en el caso de la representación por la variable Day_of_week, se detectan unos cuantos más, aquí si coincidiendo con la variable en cuestión. El problema aquí es que además de los datos atípicos que nos muestram los diagramas de cajas, tenemos que ver si existe relación entre dichas variables. En este caso, parece que la variable Pressure_heigth tiene relación con la variable Month, siendo los meses de invierno los que toman valores más bajos y los de verano más altos y por tanto ya no queda claro si realmente los datos atípicos de la variable Pressure_heigt eran realmente atípicos o simplemente son parte de la asociación observada con Month.

Variable continua con variable continua

Cuando tenemos dos variables continuas, lo que podemos hacer es dibujar un diagrama de dispersión y ver como veíamos en el ejemplo ilustrativo si dichas variables podrían tener datos atípicos

Para este caso vamos a ver Pressure_height con Ozone_reading

 plot(data$Ozone_reading ~ data$Pressure_height, main="diagrama de dispersion")

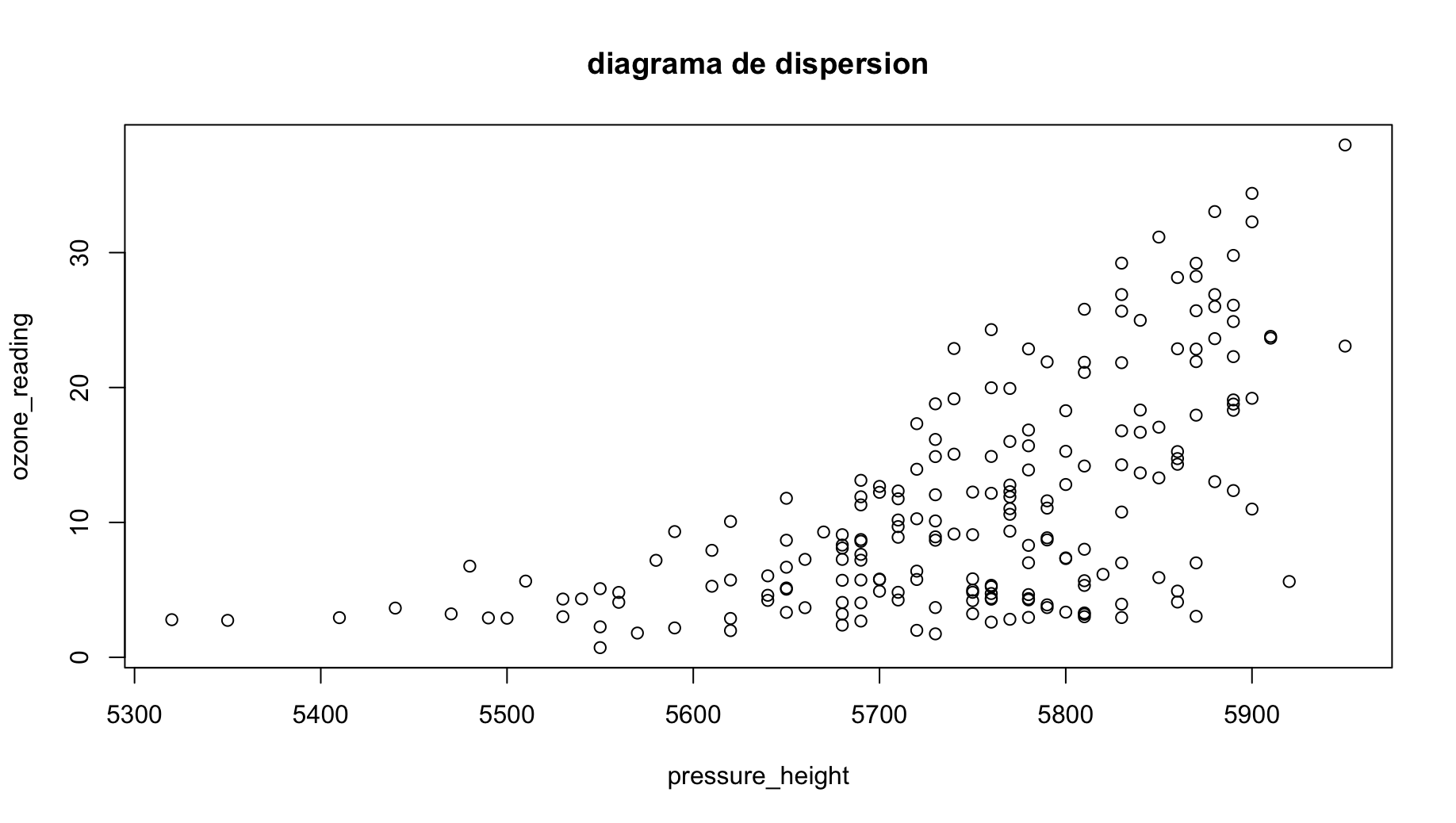
Aquí volvemos a ver los posibles outliers de la variable Pressure_height, pero también vemos como esta variable se asocia con la de Ozone_reading siendo que los valores que se veían como atípicos en el diagrama de cajas primero, se relacionan con niveles muy bajitos de la variable Ozone reading, por tanto, ¿Son datos realmente atípicos?

Considerando lo ya visto en el caso univariante y esto, vamos a dejar estos datos sin tocar.

Resumen para la detección de atípicos

1. Representar el diagrama de cajas de la variable en cuestión y calcular los valores atípicos y extremos como valores que se alejan de 1.5*IQR (atípico) y de 3*IQR (extremo).

2. Para poder ser considerados datos atípicos o extremos deben representar entre el 2-5% del conjunto de datos porque sino se trataría de datos "típicos".

3. Se puede realizar un estudio bivariado para ver si esos datos atípicos son parte de una asociación estadística o no. Si lo son, no los consideraremos atípicos.