Tratamiento de datos perdidos

Tratar de forma adecuada los datos perdidos es muy importante para los análisis posteriores. Hay dos cosas que se pueden hacer:

• Borrarlos

• Imputarlos

La decisión muchas veces vendrá dada por el número de datos perdidos, los análisis posteriores que se quieran realizar, si queremos hacer análisis univariante o multivariante, etc...

Filtrar filas con datos perdidos

Para filtrar filas con datos perdidos, podemos usar la función drop_na() del paquete dplyr.

Veamos el ejemplo con la base de datos de la epidemia de Ebola (linelist):

linelist %>% 
  drop_na() %>%     # remove rows with ANY missing values
  nrow()

## [1] 1818

Se pueden también borrar las filas solo de ciertas columnas (variables):

linelist %>% 
  drop_na(date_onset) %>% # remove rows missing date_onset 
  nrow()
  ## [1] 5632

Imputación de datos perdidos

Aunque siempre puedes analizar un conjunto de datos después de eliminar todos los valores perdidos, esto puede causar varios problemas. Aquí tienes dos ejemplos:

• Al eliminar todas las observaciones con valores perdidos o variables con una gran cantidad de datos perdidos, puedes reducir tu poder o capacidad para realizar algunos tipos de análisis. Por ejemplo, como descubrimos anteriormente, solo una pequeña fracción de las observaciones en nuestro conjunto de datos tiene datos completos en todas nuestras variables. ¡Si elimináramos la mayoría de nuestro conjunto de datos, perderíamos mucha información! Y la mayoría de nuestras variables tienen cierta cantidad de datos perdidos; para la mayoría de los análisis, probablemente no sea razonable eliminar cada variable que tenga muchos datos perdidos.

• Dependiendo de por qué faltan tus datos, el análisis solo de datos no faltantes podría conducir a resultados sesgados o engañosos. Por ejemplo, como aprendimos anteriormente, nos faltan datos de algunos pacientes sobre si han tenido síntomas importantes como fiebre o tos. Pero, como posibilidad, tal vez esa información no se registró para personas que obviamente no estaban muy enfermas. En ese caso, si simplemente eliminamos esas observaciones, estaríamos excluyendo a algunas de las personas más saludables en nuestro conjunto de datos y eso podría sesgar realmente cualquier resultado.

Es importante pensar en por qué tus datos podrían faltar, además de ver cuánto falta. Hacer esto puede ayudarte a decidir qué tan importante podría ser imputar datos faltantes y también qué método de imputación de datos faltantes podría ser el mejor en tu situación.

Tipos de datos perdidos

Aquí hay tres tipos generales de datos perdidos:

1. Missing Completely at Random (MCAR): Son datos perdidos completamente aleatorios, es decir, la ausencia de valores en un conjunto de datos es independiente tanto de otras variables observadas como de las no observadas.

   Ejemplo: la ausencia de respuestas en una encuesta no está relacionada con ninguna característica de los encuestados ni con ninguna otra variable medida en la encuesta.

2. Missing at Random (MAR): Son datos perdidos aleatorios, es decir, la probabilidad de que un valor falte puede depender de otras variables observadas, pero no de las no observadas.

   Ejemplo: supongamos que en un conjunto de datos de pacientes, la información sobre la fiebre solo falta en aquellos casos donde los médicos no tomaron la temperatura de los pacientes con ciertos síntomas específicos, como escalofríos y dolores. En este caso, la ausencia de la información sobre la fiebre no es completamente al azar, ya que está relacionada con la presencia de ciertos síntomas observados.

   A pesar de que la ausencia no es completamente aleatoria, los datos MAR son más manejables que los datos "Missing Not at Random" (MNAR), ya que, en teoría, se puede modelar y abordar la falta de manera sistemática si se conocen las variables relacionadas con la ausencia. Este es un tipo común de datos faltantes.

3. Missing not at Random (MNAR): Datos perdidos de forma no aleatoria, es decir, la probabilidad de que falte un valor depende de la variable no observada. Esto puede introducir sesgos en los datos y es más complicado de manejar. En otras palabras, la falta de un valor está relacionada con la información que falta y no puede ser modelada únicamente en función de las variables observadas.

   Ejemplo: la falta de información sobre los ingresos en una encuesta, donde las personas con ingresos más altos podrían ser menos propensas a revelar esa información.

Tratar con datos MNAR (Missing not at Random) puede ser más complicado que tratar con datos MCAR (Missing Completely at Random) o MAR (Missing at Random) porque la falta de información está relacionada con la información que falta.

La elección de la estrategia de imputación o manejo de datos perdidos a menudo depende del mecanismo subyacente que cause la pérdida de datos. Para datos MCAR, las técnicas de imputación simple, como la imputación por la media, mediana o moda, pueden ser apropiadas. Para datos MAR o MNAR, a menudo se prefieren métodos más avanzados que tienen en cuenta la relación entre las variables observadas y no observadas.

Imputación simple:

Imputación usando la media (v.continuas) o moda (v.categóricas)

Esta es la forma más sencilla de imputación cuando puedes asumir que los datos son MCAR. Si las variables son continuas puedes simplemente establecer los valores perdidos usando la media de esa variable. Por ejemplo, podemos asumir que las mediciones de temperatura faltantes en nuestro conjunto de datos son MCAR. Pero, en muchas situaciones, reemplazar los datos con la media puede generar sesgos, así que ten cuidado.

linelist <- linelist %>%
  mutate(temp_replace_na_with_mean = replace_na(temp, mean(temp, na.rm = T)))

##Gráfico para representar las diferencias  
ggplot(linelist, aes(x = temp, fill = "temp")) +
  
geom_density(alpha = 0.5) +
  
geom_density(aes(x = temp_replace_na_with_mean, fill = "temp_replace_na_with_mean"), alpha = 0.5) 

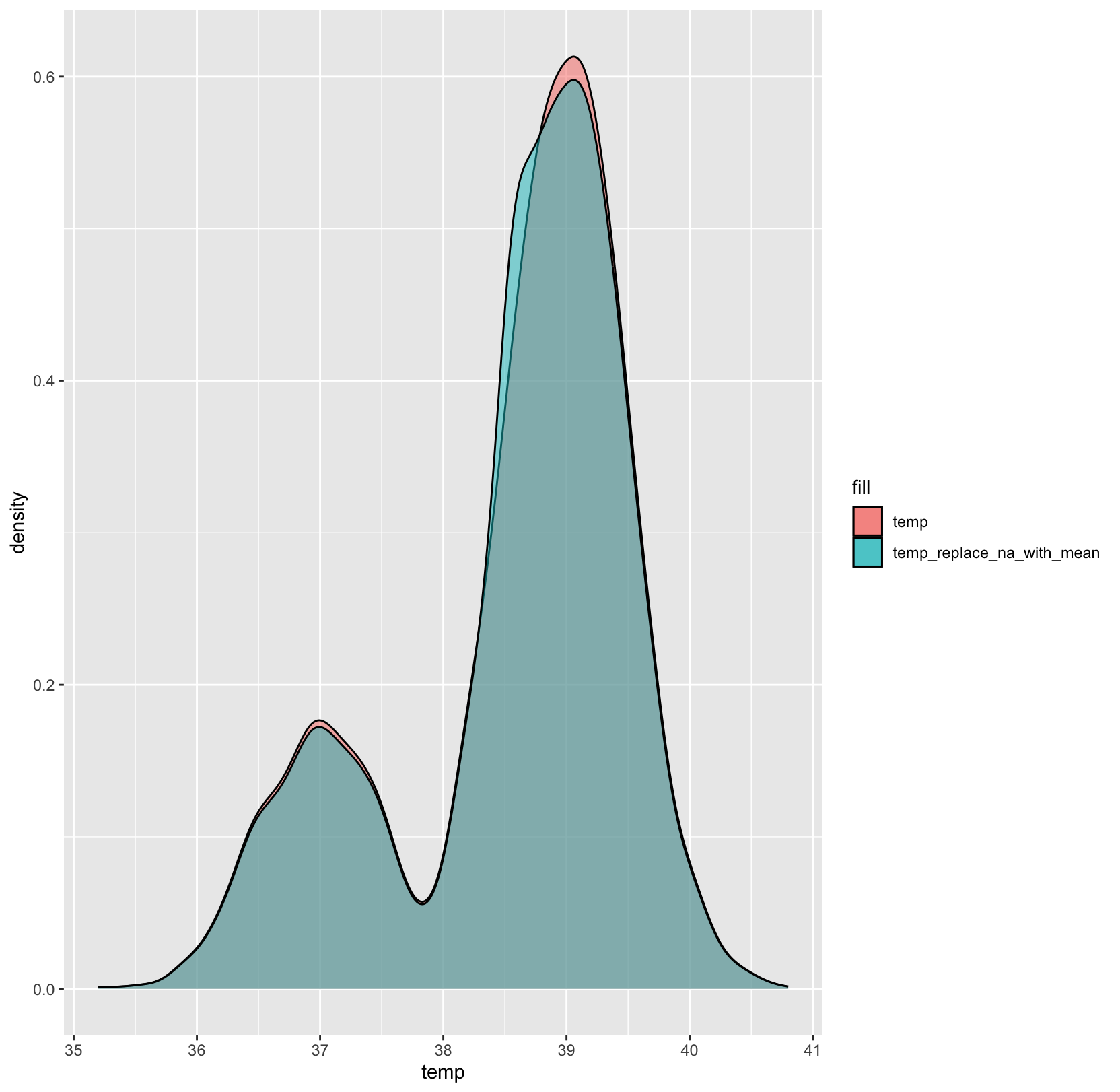
En el caso de las variables categóricas la forma de imputar valores perdidos de forma sencilla es usando la moda. Por ejemplo, los valores faltantes de la variable outcome (variable categórica) se pueden representar por la categoría más frecuente ("Death" en este caso):

#Comprobamos la categoría más frecuente
table(linelist$outcome,useNA = "always")

## Sustituímos los NA con la categoría más frecuente
linelist <- linelist %>%
  mutate(outcome_replace_na_with_death = replace_na(outcome, "Death"))
 
## Volvemos a comprobar 
table(linelist$outcome,linelist$outcome_replace_na_with_death,useNA = "always")

LOCF and BOCF

LOCF (Last Observation Carried Forward) y BOCF (Baseline Observation Carried Forward) son métodos de imputación para datos de series temporales o longitudinales. La idea es tomar el valor observado previo como sustituto de los datos perdidos. Cuando hay varios valores perdidos en sucesión, el método busca el último valor observado.

La función fill() del paquete tidyr se puede utilizar tanto para la imputación LOCF como para la BOCF (sin embargo, otros paquetes como HMISC, zoo y data.table también incluyen métodos para hacer esto).

A continuación, se muestra la sintaxis de fill() en un ejemplo de un conjunto de datos ficticio de series temporales que contiene el número de casos de una enfermedad para cada trimestre de los años 2000 y 2001. Sin embargo, los valores de los años para los trimestres subsiguientes después del primer trimestre están ausentes, por lo que necesitaremos imputarlos.

#crear la base de datos de ejemplo
disease <- tibble::tribble(
  ~quarter, ~year, ~cases,
  "Q1",    2000,    66013,
  "Q2",      NA,    69182,
  "Q3",      NA,    53175,
  "Q4",      NA,    21001,
  "Q1",    2001,    46036,
  "Q2",      NA,    58842,
  "Q3",      NA,    44568,
  "Q4",      NA,    50197)

#imputar los años que faltan
disease %>% fill(year)

Regresión lineal

Un método algo más avanzado es utilizar algún tipo de modelo estadístico para predecir cuál podría ser el valor perdido y reemplazarlo con el valor predicho. Aquí un ejemplo de cómo crear valores predichos para todas las observaciones donde la temperatura tiene datos perdidos, pero la edad y la fiebre no, utilizando una regresión lineal simple usando la fiebre y la edad como predictores.

# ajustar un modelo de regresión lineal de temperatura ~ fiebre + años
simple_temperature_model_fit <- lm(temp ~ fever + age_years, data = linelist)

#predecir los valores solo para las observaciones faltantes 
predictions_for_missing_temps <- predict(simple_temperature_model_fit,
                                        newdata = linelist %>% filter(is.na(temp))) 
                                        
## Crear una nueva variable de linelist con la temperatura imputada
linelist$temp_imputed <- linelist$temp  



# Identificar las filas con valores faltantes en temp y reemplazar con las predicciones

missing_temp_rows <- which(is.na(linelist$temp))

linelist$temp_imputed[missing_temp_rows] <- predictions_for_missing_temps



# Hacer un gráfico para comparar las observaciones


ggplot(linelist, aes(x = temp, fill = "temp")) +
  
geom_density(alpha = 0.5) +
  geom_density(aes(x = temp_imputed, fill = "temp_imputed"), alpha = 0.5) 

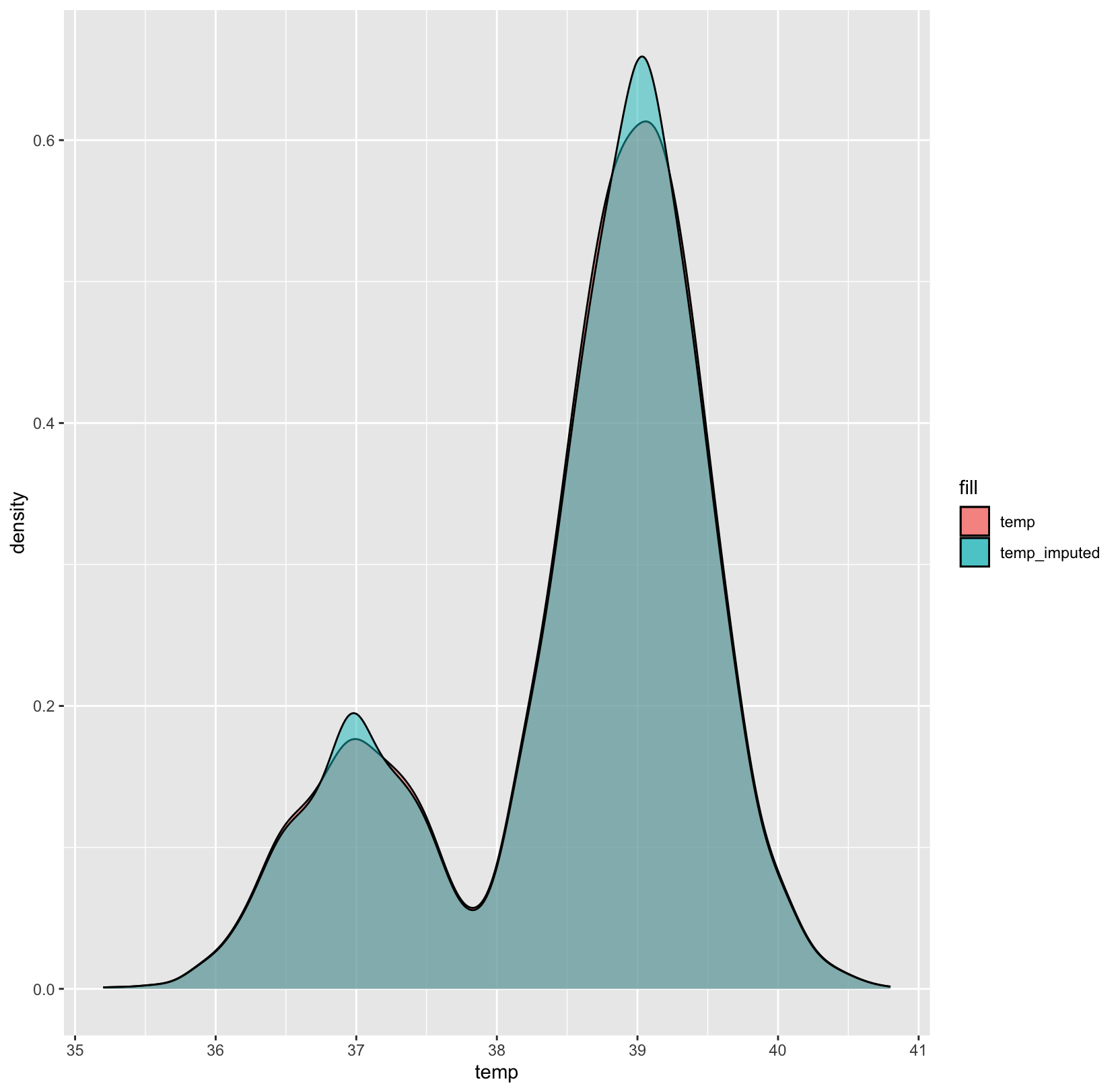
Este tipo de imputación funciona muy bien cuando los datos son MCAR, pero si los datos son MAR or MNAR habrá que tener más cuidado.

Imputación múltiple:

En R podemos usar distintos paquetes muy útiles para ello: Mmisc, missForest (usa Random Forests para imputat datos missing), and mice (Multivariate Imputation by Chained Equations). Uno de los paquetes más usados es mice.

Paquete mice:

El paquete mice en R te ayuda a imputar valores faltantes con valores de datos plausibles. Estos valores plausibles se extraen de una distribución diseñada específicamente para cada punto de datos faltante.

Vamos a utilizar los datos de airquality de R que son datos de mediciones de la calidad del aire medidos en EEUU.

data <- airquality

##Vamos a convertir unos datos del dataset en missing

data[4:10,3] <- rep(NA,7)

data[1:5,4] <- NA

##Quitamos las variables mes y día de momento

data <- data[-c(5,6)]

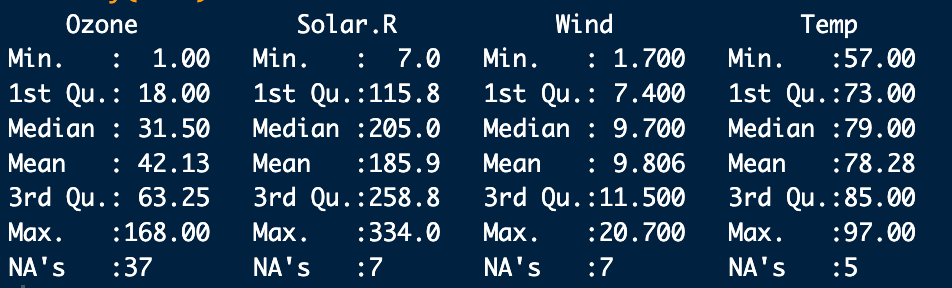
Lo primero vamos a visualizar y cuantificar como ya hemos visto los datos faltantes:

##Vamos a visualizar y cuantificar los datos missing

library(naniar)

vis_miss(data)

Observamos que la varianble ozone tiene casi el 25% de los puntos de datos faltantes, por lo tanto, podríamos considerar excluirla del análisis o recopilar más medidas. Las otras variables están por debajo del umbral del 5%, por lo que podemos conservarlas.

En cuanto a las observaciones, vemos que hay algunas que tienen datos faltantes para todas las variables. El propio paquete mice proporciona una función útil llamada md.pattern() para ver mejor el patrón de datos faltantes.

##install.packages("mice")
library(mice)

md.pattern(data)

Vemos que hay una observación para el que todas las variables son faltantes y por tanto esta observación habría que borrarla.

La función mice() se encarga del proceso de imputación. Los parámetros más importantes a tener en cuenta son:

m que representa el número de datsets que son imputadas. Por defecto es 5

maxit el número máximo de iteraciones que se van a realizar

seed que marca la semilla con la que se va a iniciar la imputación

method que indica el método de imputación

Los métodos más comunes son:

pmm (Predictive Mean Matching): Este método se utiliza para variables numéricas. Imputa los valores faltantes basándose en la distribución predictiva de la variable condicional a otras variables observadas.

logreg (Logistic Regression): Este método se utiliza para imputar variables categóricas. Utiliza regresión logística para predecir la categoría de una variable categórica faltante.

cart (Classification and Regression Trees): Este método utiliza árboles de clasificación y regresión para imputar valores faltantes.

Puedes adaptar los métodos según las características específicas de tus datos y el tipo de variables que estás imputando. Además, puedes combinar métodos para diferentes variables utilizando el argumento method de manera apropiada.

tempData <- mice(data,m=5,maxit=50,meth='pmm',seed=500)
summary(tempData)

Para visualizar la imputación de las variables en las 5 datasets imputados hacemos lo siguiente:

tempData$imp$Ozone
tempData$imp$Solar.R
tempData$imp$Wind

tempData$imp$Temp

Y para visualizar la base de datos complete hay que ejecutar la función complete():

completedData <- complete(tempData,1)

Los valores faltantes han sido reemplazados con los valores imputados en el primer conjunto de los cinco datasets. Si deseas utilizar otro, simplemente cambia el segundo parámetro en la funcióncomplete()

Para la inspección de los datos vamos a utilizar varios gráficos que nos comparan la distribución de los datos originales con los imputados:

Primero, podemos utilizar un diagrama de dispersión (scatterplot) y representar la variable ozone frente a todas las demás variables.

xyplot(tempData, Ozone ~ Wind+Temp+Solar.R,pch=18,cex=1)

Lo que nos gustaría ver es que la forma de los puntos magenta (imputados) coincida con la forma de los azules (observados). La coincidencia de formas nos indica que los valores imputados son efectivamente "valores plausibles".

Otro gráfico útil es el gráfico de densidad

densityplot(tempData)

La densidad de los datos imputados para cada conjunto de datos imputados se muestra en magenta, mientras que la densidad de los datos observados se muestra en azul. Nuevamente, bajo nuestras suposiciones anteriores, esperamos que las distribuciones sean similares.

Otra forma visual útil de observar las distribuciones se puede obtener utilizando la función stripplot(), que muestra las distribuciones de las variables como puntos individuales.

stripplot(tempData, pch = 20, cex = 1.2)

Supongamos que el siguiente paso en nuestro análisis es ajustar un modelo lineal a los datos. Puede surgir la pregunta de qué conjunto de datos imputados elegir. El paquete mice facilita ajustar un modelo a cada uno de los conjuntos de datos imputados y luego combinar los resultados.

###Ajustamos un modelo y luego hacemos un pool de los resultados

modelFit1 <- with(tempData,lm(Temp~ Ozone+Solar.R+Wind))

summary(pool(modelFit1))

La variable modelFit1 contiene los resultados del ajuste realizado sobre los conjuntos de datos imputados, mientras que la función pool() los combina todos juntos. Aparentemente, solo la variable Ozone es estadísticamente significativa.

Es importante destacar que hay otras columnas además de las típicas del modelo lm(): fmi contiene la fracción de información faltante, mientras que lambda es la proporción de la varianza total atribuible a los datos faltantes. Para obtener más información, te sugiero consultar el artículo citado al final de la página.

Recuerda que inicializamos la función mice con una semilla específica, por lo tanto, los resultados dependen en cierta medida de nuestra elección inicial. Para reducir este efecto, podemos imputar un mayor número de conjuntos de datos, cambiando el parámetro m (por defecto, m=5) en la función mice() de la siguiente manera: