Tratamiento de datos perdidos (Imputación Múltiple con MICE)
Last updated
Last updated
Imputación múltiple:
En R podemos usar distintos paquetes muy útiles para ello: Mmisc, missForest (usa Random Forests para imputar datos missing), and mice (Multiple Imputation by Chained Equations). Uno de los paquetes más usados es mice.
mice):El paquete mice en R te ayuda a imputar valores faltantes con valores de datos plausibles. Estos valores plausibles se extraen de una distribución diseñada específicamente para cada punto de datos faltante.
La imputación múltiple es un método que aborda el problema de los valores faltantes en los conjuntos de datos al generar múltiples conjuntos de datos completos, cada uno con valores imputados de manera diferente. Luego, los resultados se combinan para obtener estimaciones finales y varianzas que reflejen la incertidumbre de la imputación.
Ecuaciones encadenadas: El método MICE se basa en ecuaciones encadenadas, lo que significa que los valores faltantes de cada variable se imputan secuencialmente utilizando modelos predictivos basados en las demás variables en el conjunto de datos.
Iterativo: El proceso de imputación es iterativo, lo que significa que se repite varias veces hasta que se alcanza una convergencia. En cada iteración, se imputan los valores faltantes de una variable a la vez, utilizando los valores imputados de las otras variables en la iteración anterior.
Modelos Predictivos: Para imputar los valores faltantes, se utilizan modelos predictivos adecuados para cada tipo de variable. Por ejemplo, para variables numéricas, se pueden utilizar modelos de regresión lineal, mientras que para variables categóricas se pueden utilizar modelos de regresión logística.
En este algoritmo, de forma iterativa, se harán progresivamente cada vez mejores estimaciones de los datos faltantes. Inicialmente la primera estimación no es muy buena, pues se hace con la imputación por la media que vimos anteriormente, pero en los pasos restantes se aplica una regresión lineal entre pares consecutivos de columnas, y el procedimiento se repite una y otra vez hasta completar un número pre-definido de iteraciones. La idea es que progresivamente las estimaciones sean cada vez más precisas y se acerquen más y más al valor real
La función mice() se encarga del proceso de imputación de forma que considera todas las variables de forma múltiple y genera varios datasets imputadas de las que luego podremos hacer una media
Los parámetros más importantes a tener en cuenta son:
m que representa el número de datasets que son imputados. Por defecto es 5.
maxit el número máximo de iteraciones que se van a realizar.
seed que marca la semilla con la que se va a iniciar la imputación.
method que indica el método de imputación.
La diferencia entre el número de conjuntos de datos imputados y el número de iteraciones en el algoritmo MICE es:
Número de conjuntos de datos imputados (Multiple Imputations): En MICE, se crean múltiples conjuntos de datos imputados. La idea detrás de esto es capturar la incertidumbre asociada con la imputación de valores perdidos. Cada conjunto de datos imputado refleja una posible imputación de los valores perdidos. Este número de conjuntos de datos imputados es una decisión que el usuario debe tomar antes de ejecutar el algoritmo. Por lo general, se generan varios conjuntos (a menudo 5 a 10), lo que permite obtener estimaciones más robustas y tener en cuenta la variabilidad en las imputaciones.
Número de iteraciones: Las iteraciones se refieren a la cantidad de veces que se repite el proceso de imputación dentro de cada conjunto de datos. En cada iteración, se imputan los valores perdidos utilizando modelos estadísticos, y luego se actualizan y recalculan los valores imputados para las siguientes iteraciones. El número de iteraciones se elige para garantizar que el algoritmo converja a una solución estable. Es importante ejecutar suficientes iteraciones para permitir que el proceso de imputación se estabilice y produzca estimaciones confiables.
pmm (Predictive Mean Matching): Este método se utiliza para variables numéricas. Imputa los valores faltantes basándose en la distribución predictiva de la variable condicional a otras variables observadas.
logreg (Logistic Regression): Este método se utiliza para imputar variables categóricas. Utiliza regresión logística para predecir la categoría de una variable categórica faltante.
cart (Classification and Regression Trees): Este método utiliza árboles de clasificación y regresión para imputar valores faltantes.
Puedes adaptar los métodos según las características específicas de tus datos y el tipo de variables que estás imputando. Además, puedes combinar métodos para diferentes variables utilizando el argumento method de manera apropiada.
Ten en cuenta que todos los métodos combina la predicción con el muestreo aleatorio para generar bases de datos distintas y así poder medir una incertidumbre.
Ajuste de un modelo de regresión
Se toma la variable con valores faltantes Y y se ajusta una regresión usando las observaciones completas en función de otras variables predictoras.
Esto da un conjunto de coeficientes de regresión .
MICE usa bootstrap en cada iteración para generar variabilidad en los datos de entrenamiento.
En cada imputación se obtiene un modelo de regresión ligeramente distinto, lo que cambia las predicciones y, por lo tanto, las imputaciones.
Predicción de valores faltantes
Se usa el modelo ajustado para obtener una predicción de los valores faltantes de Y.
Estas predicciones no se usan directamente para la imputación (como en la regresión clásica), sino como referencia para encontrar valores similares en los datos observados.
Búsqueda de vecinos más cercanos
Para cada observación con un valor faltante, se buscan las k observaciones más cercanas (según la predicción de la regresión) en los datos completos.
Este número k puede ajustarse (por defecto, PMM usa k=5).
Selección aleatoria del vecino
Se elige aleatoriamente uno de esos vecinos más cercanos y se usa su valor real observado como imputación.
Este paso introduce aleatoriedad en la imputación y evita que los valores imputados sean siempre los mismos.
Vamos a utilizar los datos de airquality de R que son datos de mediciones de la calidad del aire medidos en EEUU.
Visualización y Cuantificación:
Observamos que la varianble ozone tiene casi el 25% de los puntos de datos faltantes, por lo tanto, podríamos considerar excluirla del análisis o recopilar más medidas. Las otras variables están por debajo del umbral del 5%, por lo que podemos conservarlas.
Tipos de datos perdidos
Podríamos decir según estos gráficos que los datos faltantes de Ozone y Solar.R son MCAR ya que no hay ninguna relación con las demás variables, pero los datos de Wind y Temp corresponden a datos que tienen valores bajos de Ozone pero no son todos los valores bajos de Ozone, por tanto serían MNAR ya que parece que hay una relación no observada, pero poco pronunciada.
Patrón de los datos faltantes. ¿Hay alguna observación con todo datos faltantes?
El propio paquete mice proporciona una función útil llamada md.pattern() para ver mejor el patrón de datos faltantes.
Vemos que hay una observación para el que todas las variables son faltantes y por tanto esta observación habría que borrarla.
Imputación usando el método pmm
Para visualizar la imputación de las variables en las 5 datasets imputados hacemos lo siguiente:
Y para visualizar la base de datos complete hay que ejecutar la función complete():
Los valores faltantes han sido reemplazados con los valores imputados en el primer conjunto de los cinco datasets. Si deseas utilizar otro, simplemente cambia el segundo parámetro en la funcióncomplete()
Para la inspección de los datos vamos a utilizar varios gráficos que nos comparan la distribución de los datos originales con los imputados:
Primero, podemos utilizar un diagrama de dispersión (scatterplot) y representar la variable ozone frente a todas las demás variables.
Lo que nos gustaría ver es que la forma de los puntos magenta (imputados) coincida con la forma de los azules (observados). La coincidencia de formas nos indica que los valores imputados son efectivamente "valores plausibles".
Otro gráfico útil es el gráfico de densidad
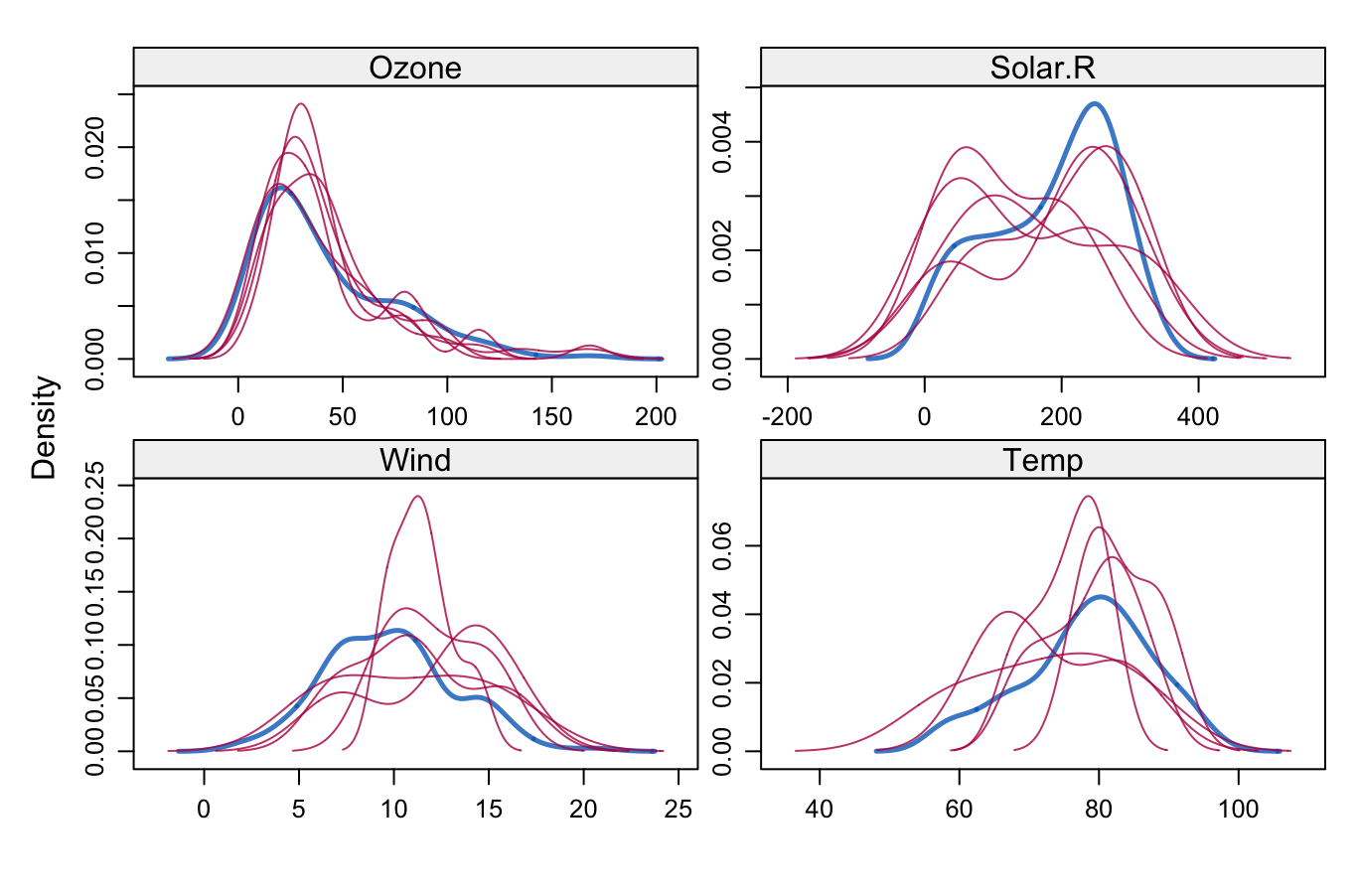
La densidad de los datos imputados para cada conjunto de datos imputados se muestra en magenta, mientras que la densidad de los datos observados se muestra en azul. Nuevamente, bajo nuestras suposiciones anteriores, esperamos que las distribuciones sean similares.
Otra forma visual útil de observar las distribuciones se puede obtener utilizando la función stripplot(), que muestra las distribuciones de las variables como puntos individuales.
Ajustar un modelo de regresión lineal
Supongamos que el siguiente paso en nuestro análisis es ajustar un modelo lineal a los datos. Puede surgir la pregunta de qué conjunto de datos imputados elegir. El paquete mice facilita ajustar un modelo a cada uno de los conjuntos de datos imputados y luego combinar los resultados.
La variable modelFit1 contiene los resultados del ajuste realizado sobre los conjuntos de datos imputados, mientras que la función pool() los combina todos juntos.
Para evaluar la calidad del ajuste con las imputaciones, se puede usar el valor fmi que proporciona la fracción de información perdida debida a los valores faltantes y el lambda que es la proporción de la varianza total atribuible a los datos faltantes. Aparentemente, solo la variable Ozone es estadísticamente significativa.
Recuerda que inicializamos la función mice() con una semilla específica, por lo tanto, los resultados dependen en cierta medida de nuestra elección inicial. Para reducir este efecto, podemos imputar un mayor número de conjuntos de datos, cambiando el parámetro m (por defecto, m=5) en la función mice() de la siguiente manera:
Calcular el
Aunque la estimación exacta del no se puede calcular como parte de la función combinada, existe una opción para calcular un pseudo basado en la transformación de Fisher-z para correlaciones y que ha sido estudiada en el contexto de múltiples imputaciones por Harel (2009) que se puede calcular con la función pool.r.squared()
