Pruebas de Normalidad

En estadística, las pruebas de normalidad desempeñan un papel fundamental a la hora de evaluar si los datos son adecuados para aplicar determinados métodos de análisis. Estas pruebas proporcionan información sobre la forma de la distribución de una variable (simetría, colas, presencia de valores extremos) y nos ayudan a decidir si es razonable asumir que los datos proceden de una población aproximadamente normal.

La normalidad es una suposición clave en muchos procedimientos clásicos, como los contrastes paramétricos de medias o los modelos de regresión, cuyos resultados (p-valores, intervalos de confianza, etc.) se derivan bajo el supuesto de distribución normal. Por ello, antes de aplicar estos métodos, es importante comprobar hasta qué punto esta suposición resulta aceptable en nuestros datos. En este tema nos centraremos en herramientas gráficas (histogramas, gráficos de probabilidad normal, etc.) y en pruebas numéricas específicas de normalidad, analizando sus ventajas, limitaciones y cómo interpretar sus resultados en la práctica.

Distribución normal

La distribución normal, también conocida como distribución gaussiana, es una de las distribuciones estadísticas más importantes en la teoría de probabilidad y estadística. Es una distribución continua que tiene propiedades matemáticas bien definidas, lo que la convierte en una herramienta fundamental en muchos análisis estadísticos.

Características de la Distribución Normal:

Forma de Campana:
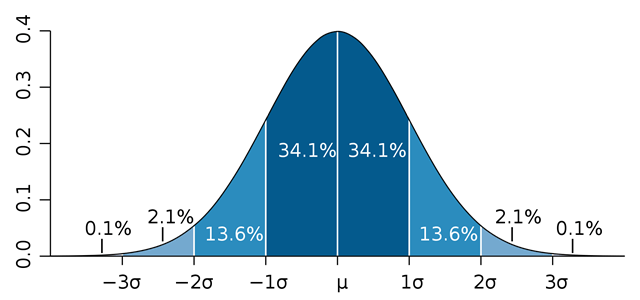
- La distribución normal tiene una forma de campana simétrica. La mayor densidad de probabilidad se encuentra en el centro alrededor de la media μ , y la probabilidad disminuye a medida que nos alejamos hacia los extremos (1σ, 2σ, 3σ, ...).
Regla Empírica (Regla 68-95-99.7):
- Aproximadamente el 68% de los datos están dentro de una desviación estándar de la media, el 95% dentro de dos desviaciones estándar, y el 99.7% dentro de tres desviaciones estándar.
Media, Mediana y Moda Igual:
- La media, mediana y moda de la distribución normal son iguales y se encuentran en el centro de la campana.
Parámetros:
- La distribución normal se caracteriza por dos parámetros: la media (μ) y la desviación estándar (σ). Estos parámetros determinan completamente la forma de la distribución.
Función de Densidad de Probabilidad (PDF):
- La función de densidad de probabilidad de la distribución normal está dada por la fórmula matemática:
$f(x) = \frac{1}{\sigma \sqrt{2\pi}} \cdot e^{-\frac{1}{2}\left(\frac{x - \mu}{\sigma}\right)^2}$
Donde:
- $f(x)$ es la función de densidad de probabilidad.
- $x$ es la variable aleatoria.
- $μ$ es la media de la distribución.
- $σ$ es la desviación estándar.

Métodos para el estudio de normalidad

Métodos gráficos

Para ver los métodos gráficos vamos a simular dos conjuntos de datos, unos siguiendo una distribución normal y otra siguiendo una distribución exponencial

##Datos simulados normales

set.seed(123)

datos_sim_norm <- rnorm(1000, mean = 5, sd = 2)

summary(datos_sim_norm)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
-0.6195  3.7434  5.0184  5.0323  6.3292 11.4821

Lo primero que vemos en los datos simulados como una distribución normal es que la media y la media son muy similares alrededor de 5 que es la media con la que se han simulado los datos.

##Datos simulados exponenciales
set.seed(123)
datos_sim_exp <- rexp(1000, rate = 0.5)
summary(datos_sim_exp)

    Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
 0.001652  0.613385  1.462333  2.059959  2.853270 14.422015

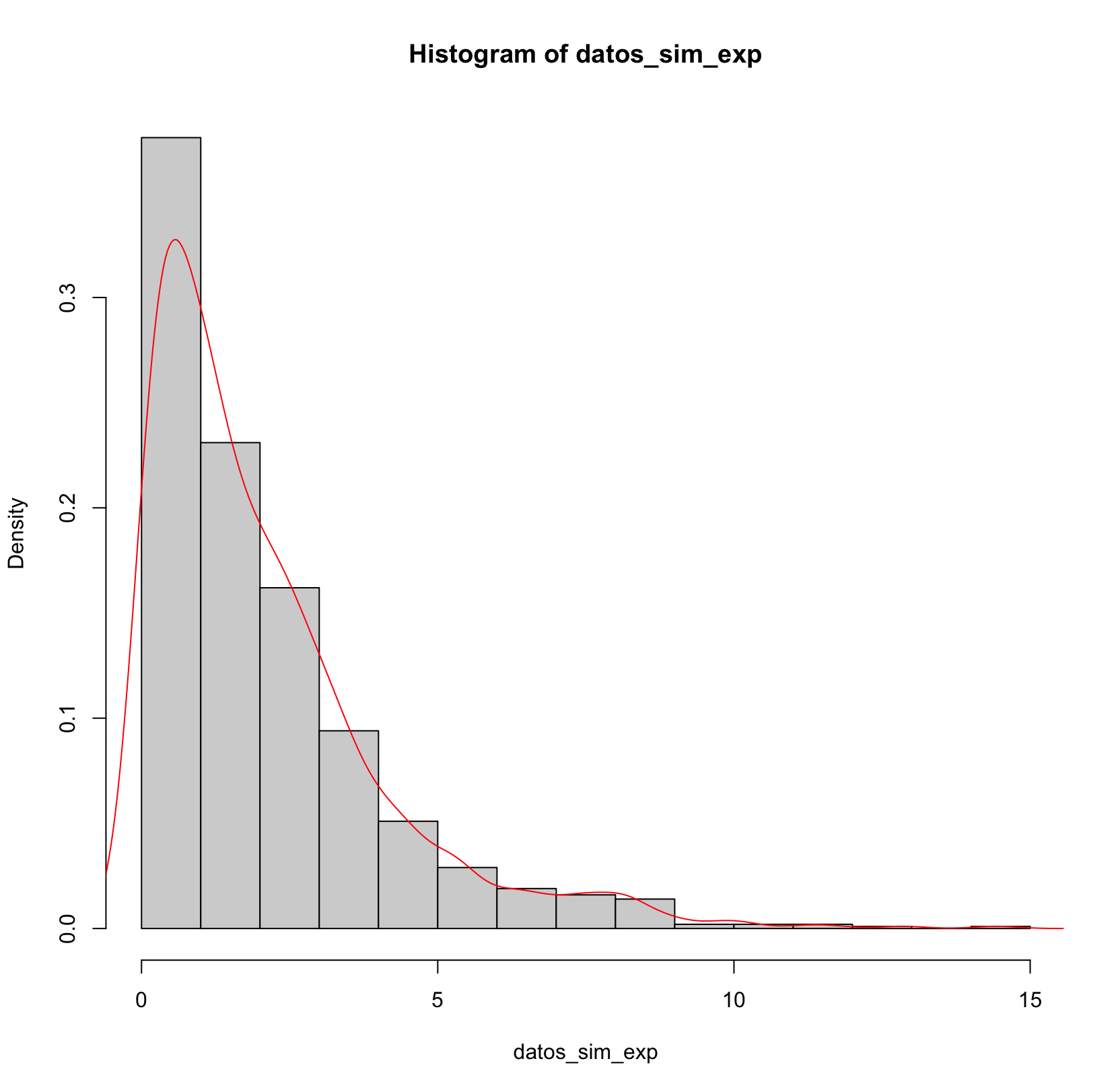
En el caso de la exponencial, ya se ve como la media y la mediana no son iguales y la media se desvía de la mediana.

Histograma

Un histograma es una representación gráfica de la distribución de los datos. Si los datos siguen una distribución normal, el histograma debería tener una forma de campana . Puedes superponer la densidad teórica de la distribución cuya media y varianza son las de la muestra.

##Histograma de los datos normales

hist(datos_sim_norm, prob = TRUE)

lines(density(datos_sim_norm), col = "red")




##Histograma de los datos exponenciales

hist(datos_sim_exp, prob = TRUE)

lines(density(datos_sim_exp), col = "red")

En el histograma de los datos normales, se ve una distribución aproximadamente simétrica, con la mayoría de los valores concentrados alrededor del centro y una forma en “campana”. La línea suave en rojo representa la densidad empírica de los datos y se ajusta razonablemente a esa forma simétrica típica de la distribución normal.

En cambio, en el histograma de los datos exponenciales, la distribución es claramente asimétrica: muchas observaciones se acumulan cerca de 0 y la cola se extiende hacia la derecha. La densidad en rojo muestra una caída rápida al principio y una cola larga, una forma muy distinta de la campana normal. Este contraste permite visualizar qué tipo de distribuciones se alejan claramente de la normalidad.

Gráfico de Probabilidad Normal (Q-Q plot)

El gráfico de probabilidad normal (Q-Q plot o quantile-quantile plot) compara cuantiles observados de un conjunto de datos con los cuantiles esperados de una distribución normal. La idea es verificar si los datos siguen o no una distribución normal.
Aquí hay una descripción del cálculo matemático detrás del Q-Q plot:

Ordenar los Datos:
- Se ordenan los datos de menor a mayor.
Cálculo de los Cuantiles Esperados de una Distribución Normal:
- Se calculan los cuantiles esperados de una distribución normal estándar. Estos cuantiles son calculados mediante la función inversa de la función de distribución acumulativa (CDF) de la distribución normal estándar. En R, se pueden obtener con la función qnorm().
Generación del Q-Q Plot:
- Se grafican los cuantiles ordenados de los datos observados contra los cuantiles esperados de la distribución normal. Si los datos siguen una distribución normal, los puntos en el Q-Q plot deberían seguir aproximadamente una línea recta.

En R, se puede usar la función qqnorm()

### Q-Q plot datos normales

qqnorm(datos_sim_norm)

qqline(datos_sim_norm, col = "red")



### Q-Q plot datos exponenciales

qqnorm(datos_sim_exp)

qqline(datos_sim_exp, col = "red")

En el Q-Q plot de los datos normales, la mayoría de los puntos se sitúan muy cerca de la recta roja, con solo pequeñas desviaciones al principio y al final. Esto indica que los cuantiles de la muestra se parecen mucho a los cuantiles teóricos de una distribución normal, por lo que la suposición de normalidad resulta razonable.

En el Q-Q plot de los datos exponenciales, los puntos se apartan de forma sistemática de la recta roja, especialmente en las colas: al principio se curvan por debajo y al final por encima de la recta. Este patrón de curvatura refleja una distribución claramente asimétrica y con cola larga, lo que indica que la distribución de los datos está lejos de ser normal.

Métodos númericos

Además de comprobar la normalidad de forma gráfica, a veces es necesario evaluar si un conjunto de datos sigue o no una distribución normal de forma numérica, mediante pruebas estadísticas.

Prueba de Shapiro-Wilk

Es una prueba de normalidad utilizada para determinar si una muestra proviene de una población normalmente distribuida. El test es especialmente eficaz para muestras de tamaño pequeño a moderado.

La prueba se plantea como un contraste de hipótesis donde:

H_0: \text{La muestra proviene de una distribución normal.} \\ H_1: \text{La muestra no proviene de una distribución normal.}

Estadístico de Prueba: El estadístico de prueba se denota como ( W ) y viene definido por:

W = \frac{\left(\sum_{i=1}^{n} a_i x_{(i)}\right)^2}{\sum_{i=1}^{n} (x_i - \bar{x})^2}

Donde:

( n ) \text{ es el tamaño de la muestra} \\ (x_{(i)} ) \text{ es el }(i)-ésimo \text{ valor ordenado de la muestra} \\ ( \bar{x} ) \text{ es la media de la muestra}\\a_i \text{ son los coeficientes de la matriz de covarianza}

El estadístico de la prueba $W$ mide el ajuste de los puntos del gráfico de probabilidad Normal a la recta.

El valor de $W$ está acotado entre 0 y 1.

Valores pequeños de $W$ tienden a rechazar la hipótesis de Normalidad.

La distribución de $W$ es asimétrica por lo que a veces valores relativamente altos de $W_n$ (como 0.9) pueden llegar a considerarse no suficientes como para aceptar Normalidad y por tanto rechazar la hipótesis nula.

Es importante destacar que la interpretación del resultado debe hacerse considerando el tamaño de la muestra entre otros factores.

###Test Shapiro - Wilk

##Datos normales

shapiro.test(datos_sim_norm)

	Shapiro-Wilk normality test

data:  datos_sim_norm
W = 0.99838, p-value = 0.4765

##Datos exponenciales

shapiro.test(datos_sim_exp)

	Shapiro-Wilk normality test

data:  datos_sim_exp
W = 0.82872, p-value < 2.2e-16

En el primero ( $p-valor=0.4765$ ): No podemos rechazar la $H_0$ y por tanto los datos siguen una distribución normal

En el segundo ( $p-valor=2.2*10^-16$ ): Rechazaremos la $H_0$ y por tanto los datos no siguen una distribución normal.

Prueba de Kolmogorov-Smirnov

La prueba de Kolmogorov-Smirnov (KS) es una prueba no paramétrica utilizada para evaluar si una muestra proviene de una distribución específica. Es decir, determina la bondad de ajuste de dos distribuciones de probabilidad entre sí. La prueba compara la función de distribución acumulativa empírica (ECDF) de la muestra con la función de distribución acumulativa teórica.

El estadístico de prueba en la prueba de KS se basa en la mayor discrepancia absoluta entre la ECDF observada y la ECDF teórica. La fórmula para el estadístico de prueba (D) es:

D = \max \left( \sup_x |F_n(x) - F(x)|, \sup_x |F_n(x-) - F(x)| \right)

donde:

es la ECDF de la muestra.
es la función de distribución acumulativa teórica.
denota el supremo (o la mayor disparidad) sobre todos los puntos en el dominio de la distribución.

En palabras, el estadístico de pruebarepresenta la mayor discrepancia entre la ECDF observada y la ECDF teórica. Cuanto mayor sea , mayor será la evidencia de que la muestra no sigue la distribución teórica.

Para el caso de usar la prueba para una distribución normal se plantea el siguiente contraste de hipótesis:

H_0: \text{La muestra proviene de una distribución normal.} \\ H_1: \text{La muestra no proviene de una distribución normal.}

Se compara el valor observado de con los valores críticos de la tabla de Kolmogorov-Smirnov para decidir si se rechaza o no la hipótesis nula.
Si el valor observado de es mayor que el valor crítico correspondiente para un nivel de significancia dado, se rechaza $H_0$ indicando que la muestra no sigue una distribución normal.

###Test Kolmogorov-Smirnov para normalidad

##Datos normales

ks.test(datos_sim_norm, "pnorm",mean = mean(datos_sim_norm), 
        sd = sd(datos_sim_norm))

	Asymptotic one-sample Kolmogorov-Smirnov test

data:  datos_sim_norm
D = 0.014963, p-value = 0.9786
alternative hypothesis: two-sided

##Datos exponenciales

ks.test(datos_sim_exp, "pnorm",mean = mean(datos_sim_norm), 
        sd = sd(datos_sim_norm))

	Asymptotic one-sample Kolmogorov-Smirnov test

data:  datos_sim_exp
D = 0.62383, p-value < 2.2e-16
alternative hypothesis: two-sided

En el primero ( $p-valor=0.9786$ ): No podemos rechazar la $H_0$ y por tanto los datos siguen una distribución normal

En el segundo ( $p-valor=2.2*10^-16$ ): Rechazaremos la $H_0$ y por tanto los datos no siguen una distribución normal.

Recuerda que el test de Kolmogorov-Smirnov es sensible al tamaño de la muestra, por lo que con muestras grandes, es más probable que encuentres diferencias estadísticas significativas. En tales casos, otros métodos y gráficos de diagnóstico pueden ser útiles para evaluar la normalidad.

¿Y qué ocurre si los datos no siguen una distribución Normal?
Podemos transformarlos para que si la sigan

Transformación Box-Cox

La transformación de Box–Cox es una familia de transformaciones propuesta por George Box y David Cox (1964) para estabilizar la varianza y aproximar los datos a una distribución normal.

Para una variable positiva $y>0$ , la transformación se define como:

y(\lambda) = \begin{cases} \frac{{y^\lambda - 1}}{{\lambda}} & \text{si } \lambda \neq 0 \\ \log(y) & \text{si } \lambda = 0 \end{cases}

Donde $y$ es la variable original y $λ$ es el parámetro de transformación.

En muchos casos los datos pueden tomar valores cero o negativos. Box y Cox propusieron entonces una versión generalizada introduciendo un parámetro de desplazamiento $\lambda_2$ :

y(\lambda) = \begin{cases} \frac{{(y+\lambda_2)^\lambda_1 - 1}}{{\lambda_1}} & \text{si } \lambda_1 \neq 0 \\ \log(y+\lambda_2) & \text{si } \lambda_1 = 0 \end{cases}

En la práctica se elige $\lambda_2$ para que $y_i+\lambda_2>0$ de manera que $\lambda_1$ es el único parámetro a estimar.

La elección de $λ$ es crucial, y la transformación de Box-Cox busca el valor de $λ$ que maximiza la normalidad y la homocedasticidad de los datos. Sin embargo, las transformaciones más habituales se describen en la siguiente tabla:

Transformación

-2

$1/y^2$

-1

$1/y$

-0.5

$1/\sqrt{y}$

$log(y)$

0.5

$\sqrt{y}$

$y$

$y^2$

La transformación $log(y)$ y $\sqrt{y}$ son apropiadas para corregir distribuciones positivamente asimétricas.

La transformación de los valores en sus recíprocos $1/y$ $1/y^2$ son adecuadas cuando existen valores muy extremos por el lado positivo.

Las transformaciones $y^2$ permiten corregir la asimetría negativa.

En la implementación de Box–Cox se estima λ y luego, si el valor óptimo es cercano a 0, 0.5, 1, etc., puede elegirse uno de estos valores por simplicidad e interpretabilidad

Para estimar el parámetro λ, los autores Box y Cox (1964) propusieron fundamentalmente dos formas: el Método de Máxima Verosimilitud y el Método Bayesiano. En el primer caso, se busca el valor de λ que maximiza la verosimilitud (o la log-verosimilitud), lo que equivale a minimizar la suma de cuadrados de los residuos del modelo ajustado con los datos transformados. Con frecuencia se explora λ en un rango entre -2 y 2.

Usando R, podemos hacer uso de la función boxcox() de la librería MASS para estimar el parámetro de transformación por estimación de máxima verosimilitud.

Aplicación a una variable:

La trasnformación box-cox se usa mucho en el contexto de la regresión lineal, pero en el punto de estudio en el que estamos ahora, sólo nos interesa buscar la normalidad de una única variable, ya que queremos dejar una base de datos lista para swer analizada en cualquier contexto.

# Instalar y cargar el paquete MASS si aún no está instalado

# install.packages("MASS")

library(MASS)


datos_prueba <- c(0.103, 0.528, 0.221, 0.260, 0.091,

           1.314, 1.732, 0.244, 1.981, 0.273,
       
           0.461, 0.366, 1.407, 0.079, 2.266)

# Histograma de los datos
hist(datos_prueba)

Para calcular el λ óptimo hay que ejecutar un modelo lineal con la función lm y pasarlo a la función boxcox de la siguiente manera:

boxcox(lm(datos_prueba ~ 1))

La log-verosimilitud (log-likelihood) mide qué tan bien se ajusta el modelo a los datos transformados. En el contexto de la transformación Box–Cox, para cada posible λ se ajusta un modelo lineal y se calcula la log-verosimilitud asociada; el λ óptimo es el que maximiza esta cantidad (equivalente a minimizar la suma de cuadrados de los residuos). En términos más simples, cuanto mayor sea el log likelihood, mejor será el ajuste de la transformación Box-Cox a los datos.

Como estamos trabajando en el contexto de una variable, la regresión lineal que usaremos se ajusta a un modelo sólo con la constante $Y=β_0+ε$ (~ 1).

En el gráfico que devuelve boxcox():

la línea vertical punteada central representa el parámetro estimado λ;
las otras dos líneas punteadas representan su intervalo de confianza al 95%.

Si el gráfico muestra que el valor 0 está dentro del intervalo de confianza del λ óptimo y, además, la estimación de λ está muy cerca de 0, la mejor opción suele ser aplicar la transformación logarítmica a los datos (véase la tabla de transformaciones habituales).

# Datos transformados
datos_prueba_trans <- log(datos_prueba)

# Histograma
hist(datos_prueba_trans)

Ahora los datos parece que puedan seguir una distribución normal, pero se puede comprobar realizando, por ejemplo, el test estadístico Shapiro-Wilk:

shapiro.test(new.x)
#W = 0.9, p-value = 0.2

En este caso, no se rechaza la hipótesis nula de normalidad.

En el caso de querer extraer el parámetro λ exacto:

# Lambda exacto

b<-boxcox(lm(datos_prueba ~ 1))

lambda <- b$x[which.max(b$y)] # -0.02
datos_prueba_trans_exact <- (datos_prueba ^ lambda - 1) / lambda

Pero si λ es muy cercano a 0, por simplicidad e interpretabilidad se suele preferir usar directamente la transformación logarítmica.

En el caso especial de tener valores negativos, podemos convertir todos nuestros datos en positivos antes de aplicar la transformación Box–Cox. Por ejemplo:

###box-cox con datos negativos

datos_sim_norm <- rnorm(1000, mean = 3, sd = 2)

datos_sim_norm_pos <- datos_sim_norm - min(datos_sim_norm) + 1  # Asegura que todos los valores de y sean positivos

hist(datos_sim_norm_pos)

boxcox(datos_sim_norm_pos~1)

¿Cuándo usar un test u otro?

Test de Shapiro–Wilk

Es el test recomendado cuando queremos comprobar si una variable sigue una distribución normal.
Tiene alta potencia para detectar desviaciones de la normalidad, especialmente en muestras pequeñas y medianas (por ejemplo, menos de 50–100 observaciones).
Es adecuado cuando la normalidad es un supuesto importante del análisis que vamos a realizar.

Limitaciones: A medida que el tamaño muestral aumenta, el test se vuelve muy sensible y puede detectar desviaciones muy pequeñas de la normalidad. En muestras grandes esto puede llevar a rechazar la hipótesis nula incluso cuando las desviaciones son poco relevantes desde el punto de vista práctico.

Test de Kolmogorov–Smirnov

Es un test de bondad de ajuste más general: compara la distribución empírica de los datos con una distribución teórica (no sólo la normal).
Puede utilizarse con muestras más grandes, especialmente cuando se quiere contrastar una distribución específica y la normalidad no es el foco principal.

Limitaciones:

En su versión estándar, asume que los parámetros de la distribución teórica son conocidos; Para el caso concreto de normalidad, suele tener menos potencia que el test de Shapiro–Wilk, por lo que puede pasar por alto algunas desviaciones.

En cualquier caso, la decisión no debe basarse sólo en un p-valor: es fundamental combinar los tests estadísticos con herramientas gráficas (histograma, Q–Q plot) y realizar una evaluación global de la normalidad.

Ahora vamos a realizar los siguientes ejercicios:

Ejercicio 4.1: Pruebas de Normalidad

PreviousIntroducción NextEjercicio 4.1: Pruebas de Normalidad

Last updated 1 day ago